Causality Discovery

Introduction to Causality

Definition

• Causality is the influence one event (cause) has on another (effect).
• It implies that changes in the cause lead to changes in the effect, forming a non-random link.

Key Characteristics of Causality

• Directionality: A causes B, but B does not necessarily cause A.
• Mechanism: Changes in the cause generate changes in the effect.
• Counterfactuals: Considers what would happen to the effect if the cause did not occur.

Causality Discovery

Methods

• Experiment-based approach
  • Control experiment: Intervention causes changes in outcomes,
  • In many cases too expensive, too time-consuming, or even impossible.
• Data-based approach

Overview of Data-based Causal Discovery Methods

Methods

• Constraint-based methods
  • PC
  • FCI
• Score-based methods
  • GES (Greedy Equivalence Search)
• Functional Causal Models
  • Linear, Non-Gaussian Model
  • Non-linear Methods
• Hybrid Methods
  • SELF (Structural Equational Likelihood Framework)
  • FRITL (Functional Representation with Independent Triad and Likelihood)

Constraint-Based Methods

Assumptions

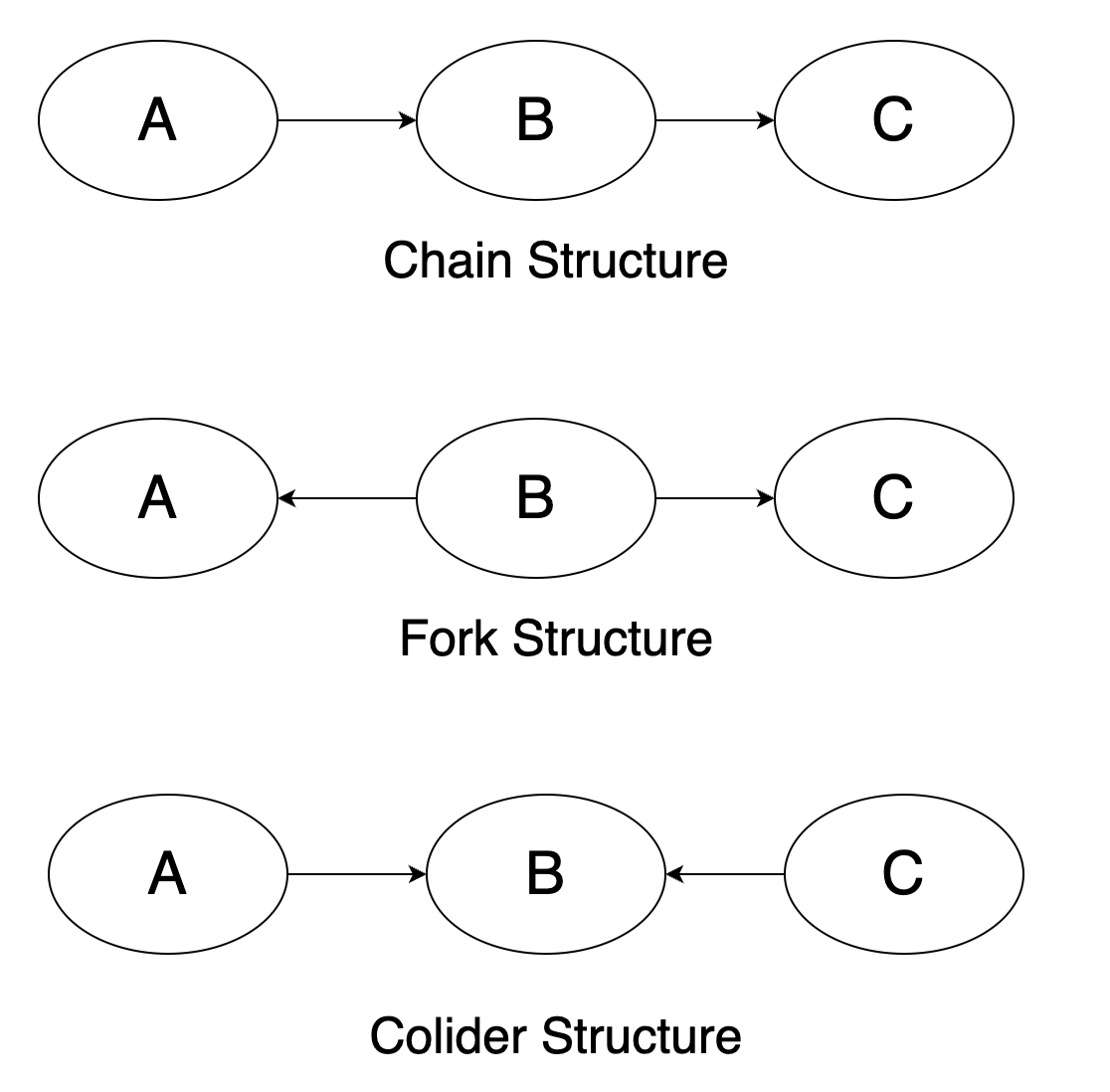
• Causal Markov Assumption: A variable $X$ is independent of every other variable (except $X$'s effects) conditional on all of its direct causes.
• Causal Faithfulness Assumption: For all observed variables, $X_i$ is independent of $X_j$ conditional on variables $Z$ if and only if the Markov Assumption for $\mathcal{G}$ entails such conditional independencies.

Limitations

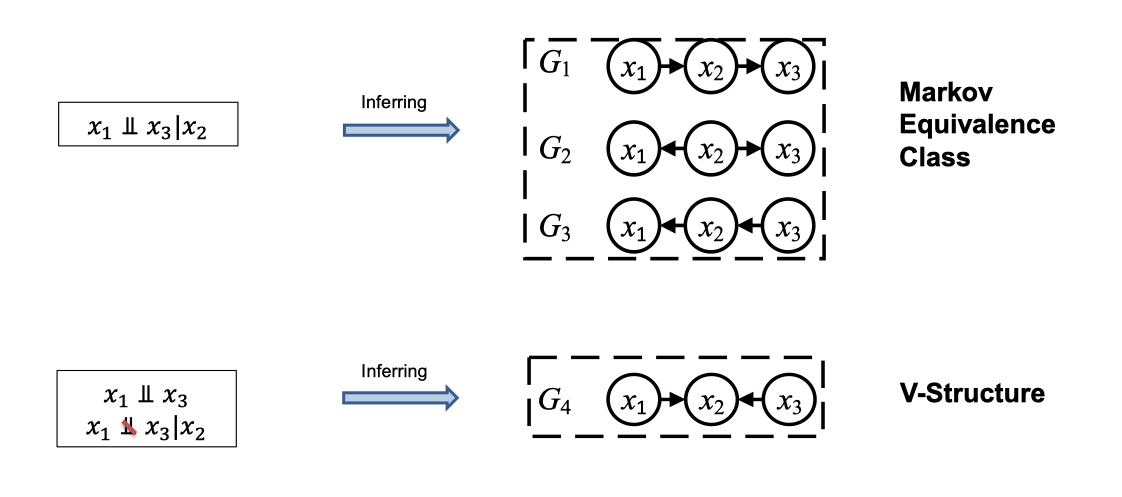
• DAGs within the same Markov Equivalence Class cannot be distinguished solely based on conditional independence relationships.

Constraint-Based Method: PC Algorithm

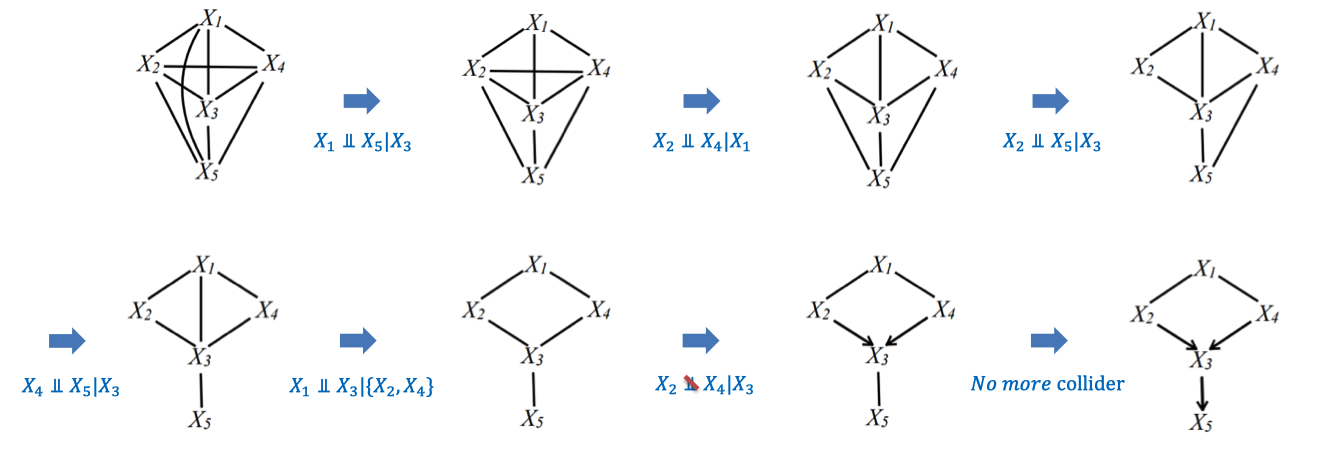
1. Initialize Graph: Start with a fully connected undirected graph.
2. Edge Removal: Test conditional independence for each pair of variables given subsets of other variables. Remove edges where conditional independence is found.
3. Identify Colliders: Orient edges for v-structures $(X\to Z\leftarrow Y)$ where $X$ and $Y$ are independent unless conditioned on $Z$.
4. Orient Remaining Edges: Use orientation rules to direct undetermined edges.
5. Output CPDAG: The result is a CPDAG representing the Markov Equivalence Class.

PC Algorithm Example

PC Algorithm Limitation

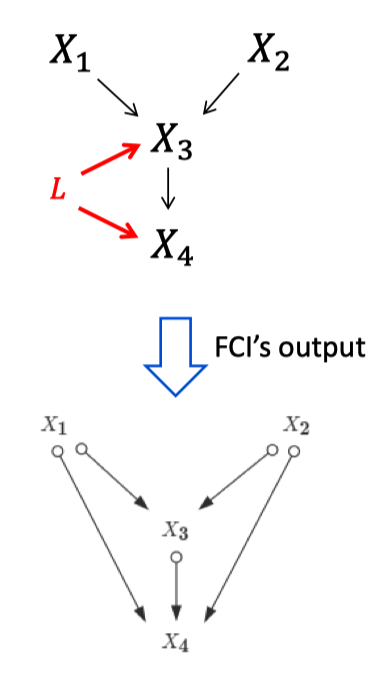
• Limitations: Unable to deal with latent confounders.

Constraint-Based Method: FCI Algorithm Process

1. Initialize Graph: Start with a fully connected undirected graph over all observed variables.
2. Edge Removal: Test conditional independence between each pair of variables given subsets of other variables.
3. Identify Colliders: Identify v-structures $(X\to Z\leftarrow Y)$.
4. Propagate Edge Orientations: Apply orientation rules to propagate edge directions.
5. Handle Ambiguous Relationships: Determine possible orientations considering latent variables.
6. Output PAG: The result is a Partial Ancestral Graph (PAG).

Functional Causal Models (FCMs)

Assumptions

1. Independent noise assumption: Independence between the causes $X$ and noises $E$.
2. Independent mechanism assumption: Independence between the causes $X$ and process $f$.

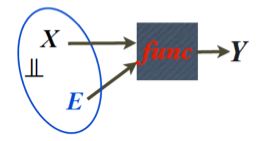
Independent Noise (IN) Condition

• Causal Asymmetry in the Linear non-Gaussian Case: $Y=\alpha X+E$, where $X\to Y$.

Functional-Based Methods: LiNGAM

LiNGAM Model

• LiNGAM can be expressed as:$$\mathbf{X}=\mathbf{B}\mathbf{X}+\mathbf{E}$$
• Assumptions:
  • $\mathbf{X}$: observed variables.
  • $\mathbf{B}$: connection weights.
  • $\mathbf{E}$: non-Gaussian noise vector.

LiNGAM: Analysis by ICA

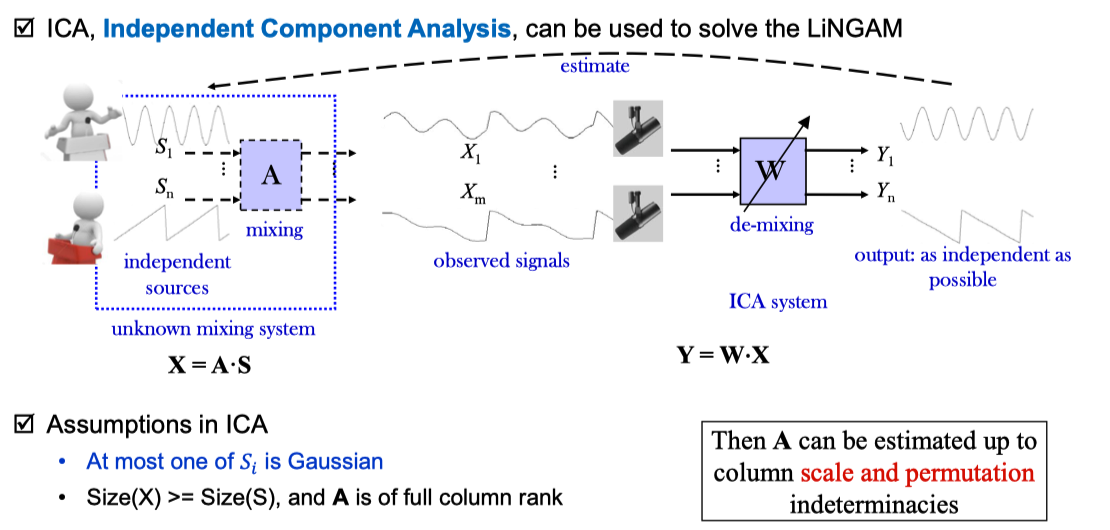
LiNGAM Example

$$\left[\begin{array}{c}{E}_1\\ E_3\\ E_2\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ -0.5& 1& 0\\ 0.2& -0.3& 1\end{array}\right]\left[\begin{array}{c}{X}_2\\ X_3\\ X_1\end{array}\right]$$$$\Rightarrow \{\begin{array}{l}{X}_2=E_1\\ X_3=0.5X_2+E_3\\ X_1=-0.2X_2+0.3X_3+E_2\end{array}$$

Functional-Based Methods: PNL (post-NonLinear method)

• PNL Model:

  $$v_j=f_2(f_1(v_i)+n_j)$$
  • $v_i$ and $n_j$ are independent.
  • $f_1$ is a non-constant smooth function.
  • $f_2$ is a reversible smooth function.

Hybrid Methods

• Hybrid Approach: Combines constraint-based and functional approaches.
• Examples:
  • SELF (Structural Equational Likelihood Framework)
  • FRITL (Functional Representation with Independent Triad and Likelihood)

Comparison of Methods

	PC	FCI	GES	LiNGAM/PNL/ANM	SELF	FRITL
Faithfulness assumption required?	Yes	Yes	Some weaker condition required (not totally clear yet)	No	No	No
Specific assumptions on data distributions required?	No	No	Yes (usually assumes linear-Gaussian models or multinomial distributions)	Yes	Yes	Yes
Properly handle confounders?	No	Yes	No	No	No	Yes
Output	Markov equivalence class	Partial ancestral graph	Markov equivalence class	DAG as well as causal model (under the respective identifiability conditions)	DAG with likelihood-based causal structure (assumes observed variables)	DAG or PAG, refined with ICA and Triad condition for latent confounders

---

Thank You for Listening!